NMR 이란?

우리말로 핵 자기공명이라고 부르는 NMR(Nuclear Magnetic Resonance)현상은 IR(Infrared)이나 UV(Ultraviolet) 분광학과 같은 또 다른 하나의 흡광 분석이다. 다시 말해 적당한 조건 하에서 라디오 파(radio frequency : ~ 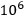Hz)를 시료에 조사하면 시료가 이 라디오파를 흡수하여 일어나는 현상이다. 이때 흡수되는 주파수(frequency)와 흡수되는 양(intensity)을 기록하면NMR 스펙트럼(spectrum)이 된다. 여기에서 적당한 조건이란 시료를 자기장(magnetic field)속에서 놓아두는것을 말한다. 결국 NMR 분광학을 위해서는 자석(magnet)과 라디오 파(rf)가 있어야 한다.

분자들은 너무나 작아서 이들을 직접 관찰하고 연구하는 것은 불가능하다. 그러므로 이들을 관찰하기 위하여 과학자들은 오래 전부터 여러 가지 간접적인 방법들을 사용해 왔으며 지금도 계속 새로운 방법들을 고안해내고 있다. 이러한 간접적인 방법들은 예를 들자면 분자 속에서 결합(bonding)을 이루고 있는 원자들간의 진동과 회전(vibration-rotation)을 이용할 때는 적외선(infrared)분광법이 되고 이들 분자들 속에 있는 전자(electron)들의 전이(transition)를 이용 할 때는 자외선(ultraviolet)분광법이라 불린다.

NMR(Nuclear Magnetic Resonance)은 이들 분자들을 관찰하는 여러 가지 간접적인 방법들 중 하나에 해당한다고 생각하면 되고 이때 관찰에 이용되는 것은 분자를 이루고 있는 원자핵들의 자기적인 성질(magnetism)이다. 바로 이 핵들의 자기적 성질이 NMR 실험을 가능하게 하는 근본이므로 가장 기본적인 NMR 현상을 이해하기 위하여 제일 먼저 핵들의 자기적 성질과 이들 핵이 자기장 속에서 어떻게 운동하는지 공부하도록 한다.

1. 원자핵의 자기적 성질

먼저 NMR의 현상을 나타내는 근원적 존재인 핵의 자기적 성질에 관해서 살펴보자.

이미 기초물리학에서 배운 것과 같이 모든 핵(nucleus)은 전하(charge)를 가지고 있다. 전하를 가지고 있는 핵은 각 운동량, P(angular momentum)를 가지며 이것은 전하를 가진 핵이 핵의 중심을 통과하는 축의 주위를 회전하는 것으로 설명할 수 있다. (그림1-1) 전하를 가진 핵이 회전한다고 하는 것은 폐쇄 회로에서 전로(current)가 흐르고 있는 것과 같다고 생각할 수 있다. 즉 폐쇄회로에서의 전류(i)는 자기장(magnetic field)을 형성하게 된다(그림1-1).

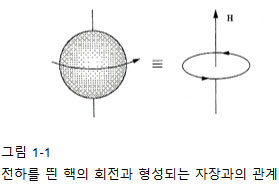
그러므로 전하를 가진 핵의 회전은 자장 즉 방향성을 가지는 자기 쌍극자(magnetic dipole)를 형성한다. 이때 생성된 자기쌍극자의 크기를 핵 자기 모멘트, (unclear magnetic moment)라고 부른다. 이러한 관계의 설명을 위해 핵 스핀, I(unclear spin)와 핵 자기 모멘트, µ(unclear magnetic moment)는 각각 식1-1과 1-2로 표시된다.

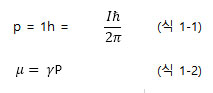
핵 스핀(줄여서 스핀이라고도 부름) 또는 핵 스핀 양자수(unclear spin quantum number) I는 정수(integer)이거나 반 정수(half-integer)의 값을 가진다. 핵 스핀 I=0라는 것은 식 1-1과 1-2에서 곧 핵 자기 모멘트가 없다는 것을 나타낸다.

이와 같은 핵은 원자번호(atomic number)와 원자량(atomic mass)이 짝수인 것들이다.

예를 들면 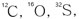등과 같은 핵들이 이들종류에 속한다. 즉, 이러한 종류의 핵들은 NMR 현상을 나타내지 못한다. 반대로 NMR 현상을 나타낼 수 있는 핵들은 핵의 원자량이 홀수일 때 반정수의 핵 스핀을 가지는 것과 원자량이 짝수이고 원자번호가 홀수일 때 정수의 핵 스핀 값을 가지는 것들이다.

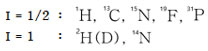
이 이외에 핵 스핀의 값이 1보다 큰 것들도 있는데 이러한 핵들로는 등을 예로 들 수 있으며 이것들 역시 NMR 현상을 나타낼 수 있다.

따라서 NMR 현상을 나타내는 모든 핵들은 I ≠ 0 의 조건을 만족시키면 되는 것이다.

식 1-2에서 𝜸는 자기회전 비(gyromagnetic ratio)라고 불리우며 이것은 핵이 가지는 고유의 값이다. 즉 실험적으로 구해야 하는 값이다. 뒤에서 다시 언급이 되겠지만 𝜸의 값이 크면 결국 핵 자기 모멘트가 커지며 이것이 각 핵들의 NMR 현상의 주파수를 결정하게 된다. 지금까지 우리는 핵이 전하를 띠고 회전하는 작은 조각으로 간단하게 가정하여 설명하였다. 비록 이 설명이 정성적이기는 하지만 식 1-1과 식1-2를 잘 설명해 준다.

2. 자기장 속에서 핵의 성질

이미 서론에서 언급한 것과 같이 NMR은 흡광(absorption) 분석의 일종이다. 즉 여러 에너지 상태에 놓여 있는 핵들이 각각의 에너지 준위(energy state)의 차이에 해당하는 에너지를 흡수할 때 전이(transition)가 일어나게 된다. NMR 현상을 일으키기 위해서는 에너지 준위들의 에너지 차이를 나게 만들어야 한다. 여러 분광학이 그렇듯이 NMR을 정확히 설명하기 위해서는 양자역학(Quantum mechanics)의 도입이 필요하다. 여기에 간단한 양자역학을 도입하면 스핀 양자수가 I인 핵은 2I+1개의 불연속적인 양자상태(m)을 가진다. 이들은 외부의 자기장이 없으면 에너지 상태가 같지만 일단 자기장 속에 놓이면 에너지 상태가 달라지게 된다. 이와 같은 상황을 양성자( 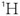, I = 1/2)의 경우로 예를 들면 2개의 에너지 상태가 존재하게 된다 (그림 1-2).

즉, 외부의 자기장이 같은 에너지 상태(degeneracy)를 분해시키게 되며 이것이 우리가 원하는 것이 되는 것이다. 이와 같은 에너지 상태의 분해 현상을 지만 효과(Zeeman effect)라고 한다. 이때 낮은 에너지 상태를 +1/2또는 𝜶, 높은 에너지 상태를 - 1/2 또는 𝜷라고 하며 두 에너지 상태의 에너지 차이, ∆E는 사용된 외부의 자기장(Ho)의 크기에 비례하게 된다. (식 1-3)

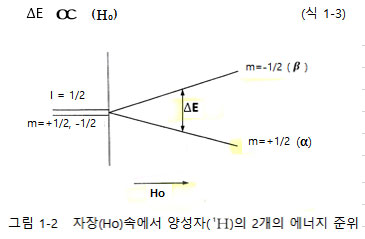
즉 외부의 자기장의 세기가 크면 클수록 두 에너지의 차이, △E는 점점 커지게 되며 이로 인한 NMR 실험상의 장점은 여러가지가 수반된다. 첫째로 감도(sensitivity)의 문제를 생각해 보기로 하자. 물이 높은 곳에서 낮은 곳으로 흐르는 것과 같이 NMR의 현상을 나타낼 수 있는 핵이 자기장속에 놓일 때, 높은 에너지 상태보다는 낮은 에너지의 상태에 더 많은 핵들이 분포되게 된다. 이때 분포되는 결과는 정량적으로 볼쯔만 방정식(Boltzmann equation)에 의하여 예측될 수 있다. 이해를 쉽게 하기 위해서 I = 1/2 즉 앞에서 예로 든 두 에너지 상태가 존재하는 상황을 고려하자. 높은 에너지 상태에 존재하는 핵의 수를 n+, 낮은 에너지 상태에 존재하는 핵의 수를 n_ 라고 한다면 상대적인 분포는 식 1-4로 표시된다. 여기에서 R(1.987 cal.)은 기체상수이며 T는 절대 온도이다.

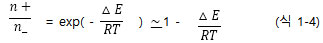
식 1-4의 정량적인 고찰은 그만 두고 먼저 정성적으로 살펴보면 n_ , 즉 낮은 에너지 상태에 분포되는 핵의 수는 △E가 크면 클수록 많아지게 된다. 모든 분광학의 기본이론과 같이 NMR 현상도 낮은 에너지 상태에 존재하는 핵들이 에너지를 흡수하여 높은 에너지 상태로 전이(transition)하는 것이므로 낮은 에너지상태에 있는 핵의 수가 많으면 많을수록 NMR의 감도(sensitivity)는 좋아지는 것이다.

흔히 NMR은 다른 분광학과 비교해서 감도가 매우 낮은 단점을 가지고 있다고 한다. 실제로 NMR 실험을 위한 시료의 양을 살펴보도록 하자. 우리가 흔히 볼 수 있는 NMR중 자장의 크기가 가장 작은 60MHz 양성자(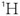)NMR의 경우 수십 mg의 시료가 필요하게 된다. 이 정도의 양은 다른 분광학 즉, IR이나 UV를 위해서 사용되는 양의 수십 배나 수백 배 또는 수천 배의 양이라고 할 수 있다.

그러면 왜 이렇게 많은 양의 시료가 필요한가를 식 1-4를 사용해서 설명해 보기로 하자.

양성자(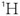)NMR일 경우 60 MHz NMR 이란 자장의 세기는 14,092 가우스(gauss)에 해당한다. 이때 △E = 0.005 calories/mole이 되며 상온에서 RT = 592 calories/mole의 값을 가지게 된다. 이 값을 대입하면 △E/RT = 1 X 10 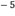이 되며 이것은 식 1-4 로 부터 핵 200,001개를 가진 시료가 60MHz NMR 자장 속에 놓여진다면 n_ = 100,001, n+ = 100,000 씩을 각각 가지게 된다는 결론을 얻을 수 있다.

즉, 낮은 에너지 상태에 있게 되는 핵은 단지 1개가 더 존재하게 된다. 이렇게 계산된 다른 에너지 상태에 있는 핵의 존재 비를 UV 분광학에서 사용되는 전자에너지 준위(electronic energy level) 그리고 IR에서 사용되는 진동에너지 준위(vibrational energy level)와 비교해 보자.

전자에너지 준위는 높은 에너지 준위와 낮은 에너지 준위의 차이가 상온에서 매우 크기 때문에 모든 분자들이 낮은 에너지 상태에서 존재한다. 그리고 진동에너지 준위에서는 단지 수 퍼센트 (%)에 해당되는 분자만 높은 에너지 상태에 존재하게 된다. 바로 이러한 차이가 NMR분광학이 다른 분광학에 비교하여 감도가 낮은 이유가 되는 것이다. 서론에서 언급한 바와 같이 현재 사용되고 있는 NMR은 900 MHz까지 있다고 했는데 이와 같이 큰 자장의 NMR이 바로 두 에너지의 차이인 △E를 커지게 함으로써 낮은 에너지 상태에 존재하는 핵의 수를 증가시키는 것이다.

실제로 이와 같이 큰 자장의 NMR에서는 보통의 유기 화합 물의 양성자(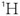)NMR을 얻기 위해서는 시료의 양은 𝝁𝐠이라도 충분한 양이라고 할 수 있다. (분자량에 따라서 다를 수 있음). 이와 같이 스펙트럼의 감도를 증가시키기 위해서 외부의 자장을 크게 하는 것 이외에 식1-4를 보면 우리는 또 다른 방법을 찾을 수 있다. 즉 상수R은 변화시킬 수 없지만 온도 T는 변화시킬 수 있다. 즉 온도를 내리면 낮은 에너지 상태의 핵의 수를 증가시킬 수 있게 된다. 이 방법은 이론상으로는 가능하지만 뒤에서 공부할 이완 시간의 지연 등 몇가지 단점들을 갖는 현상들로 인하여 실용적으로는 많이 사용되고 있지 않다.

3. 공명(Resonance) 현상

자기모멘트를 가지는 핵이 자기장 속에 놓일 때 그림 1-2에서와 같이 에너지의 차이 △E를 갖는 각기 다른 준위로 분포된다는 것을 보았다. 이제 이렇게 분포된 핵들이 어떻게 에너지를 흡수하는 가를 살펴보기로 하자. 다른 분광학에서와 마찬가지로 두 에너지 준위 사이에서 전이가 일어나게 하려면 두 에너지 준위 사이의 에너지 차이인 △E를 공급해 주어야 한다.(식 1-5)

여기에서 진동수, ν를 자장의 세기가 Ho인 자기장의 관계로 바꾸면 식 1-6으로 주어진다.

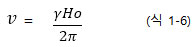
식 1-6이 NMR의 자장과 라디오 파 진동수와의 관계를 나타내는 기본식이다. 즉 양성자(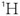) NMR일 경우 14,092 가우스(Gauss)의 자장 속에 시료를 놓으면 낮은 에너지 상태에 있는 핵들을 높은 에너지 상태로 전이시킬 때 필요한 진동수가 60 MHz(60 megacycles/sec)가 되는 것이다. 이 진동수가 바로 라디오 파(rf)의 영역에 속하는 것이며 NMR 기기의 명칭을 붙일 때 자장의 세기로 말하지 않고 바로 이 진동수의 이름을 붙이게 된다.

(일반적으로 NMR 기기는 양성자(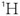)의 진동수로 명칭한다. 즉 300 MHz NMR이라고 하는 것은 양성자의 진동수를 나타낸 것이며 그러므로 이 기기에서 탄소는 75 MHz가 된다). 결국 자장의 세기가 커지면 △E는 커지고 식 1-6의 관계에 의해서 라디오 파의 진동수가 점점 커지게 된다.

보통 많이 사용되는 300 MHz NMR의 경우 자장의 세기는 식 1-6에 의해 7.05 테슬라(Tesla)가 된다. (1 테슬라는 10,000 가우스(Gauss)) 그러면 라디오 파를 어떻게 주입시키며 어떻게 전이가 일어나는가를 살펴보자.

이것은 고전 역학으로 잘 설명되므로 우리도 이것을 사용해 보자. 자전(spinning)하고 있는 핵은 자기장의 세기 Ho인 외부의 힘을 받으면 핵의 자전에 의해서 생긴 자기 쌍극자(magnetic dipole)가 외부의 자장과 일치하지 못하고 외부자장 축의 주위를 세차운동(precession)하게 된다. 이것을 그림 1-3으로 표시하였다.

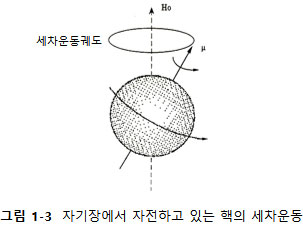
우리는 이것을 이해하기 위하여 이 현상을 흔히 지구의 자장에 의한 자이로스코프(gyroscope)의 운동에 비유한다. 이 세차 운동을 수식으로 표시하기 위하여 식 1-6을 다시 정리하면 1-7로 표기할 수 있으며 식 1-7은 다시 1-8로 변형될 수 있다.

세차 운동의 각 속도(angular velocity)는 라모어 진동수(Larmor frequeney,ωo)라고하며 이것은 식 1-8에서 보듯이 핵 고유의 값인 자기회전 비(𝜸)와 외부의 자장(Ho)에 의해서 결정된다. 바로 식 1-8을 공명조건이라 하며 이 라모어 진동수와 똑같은 진동수를 외부로부터 주입했을 때 핵은 에너지를 흡수하여 높은 에너지 상태로 전이가 일어나게 되며 이것을 공명(resonance)이라고 부른다. 이 현상은 물론 양자 역학의 법칙을 만족시킨다. 양성자()의 경우를 예로 들면 +1/2 상태에서 - 1/2 상태로의 전이는 결국 양자역학에서 선택 규칙 (selection rule)인 △m = ±1을 만족시키고 있다.

양자역학에서는 낮은 에너지 상태에서 높은 에너지 상태로 일어나는 전이 뿐만 아니라 반대로 높은 에너지 상태에서 낮은 에너지상태로 일어나는 전이도 그 확률은 같다고 알려져 있다. 즉 NMR현상은 위의 두 상황이 다 일어나고 있지만 앞에서의 언급과 같이 낮은 에너지 상태에 있는 핵의 수가 조금(미량이지만) 더 많기 때문에 모든 것이 상쇄되고 남은 핵의 전이가 피크(peak)로 나타나게 된다. 만약 이때의 피크를 +라고 정한다면 NMR의 현상 그 자체가 항시 낮은 에너지 상태의 핵 수가 많기 때문에 일어나는 현상으로 우리는 +피크만을 생각할 수 있을 것이다. 그러나 높은 에너지 상태에서 낮은에너지 상태로의 전이가 증명될 수 있는 실험들, 즉 피크가 음으로 나타나는 실험들은 제5장polarization transfer라는 실험들에서 실제로 볼 수 있다. NMR의 공명현상에서 다른 분광학과 다른 특이한 현상중의 하나는 한 종류의 핵이 전이가 일어날 확률은 그 핵이 존재하는 어떠한 환경에서도 같다는 것이다. 다른 의미로 핵이 양성자()라면 이 양성자가 어떠한 분자에 있는 양성자라 해도 NMR의 전이의 확률은 같다는 것이다.

이 현상의 차이점을 IR분광학의 현상과 비교해 보자.

IR분광학에서 탄소와 산소의 이중결합(C=O)과 탄소와 탄소의 이중결합(C=C)은 같은 이중결합이지만 흡수 피크의 세기(intensity)는 크게 다르다. 탄소와 탄소의 이중결합(C=C)만을 비교하더라도 그 주위의 환경에 따라서 즉 어떠한 분자내의 이중결합이냐에 따라서 그 흡수 피크의 세기가 틀려지게 된다. 이것은 피크의 적분이 정량분석을 하기위하여 사용될 수 없다는 것을 말해준다. 이와는 반대로 NMR 피크들 세기는 정확히 그 피크에 해당되는 핵의 상대적인 수를 나타내게 된다. 즉 정량분석에 사용될 수 있다는 것이 또 다른 장점이 된다.

이제 라모어 진동수(Larmor frequency, ωo)에 해당되는 라디오파를 어떻게 주입시키는지를 살펴보자.

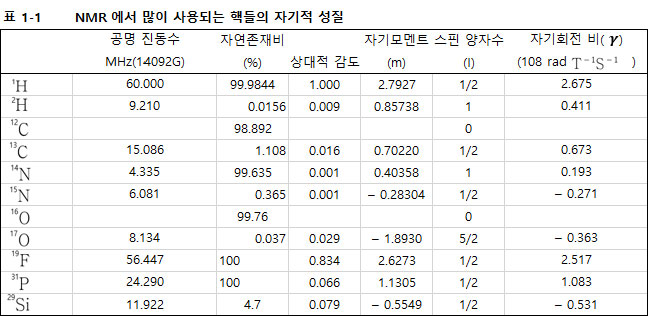
그림 1-4는 안정하고 강한 자장 속에 놓인 양성자()가 세차운동을 하고 있으며 이때 라디오파 발생기에서 주입되는 약한 자장인 H1 은 코일(transmeter coil)을 통해서 반드시 직각인 방향에서 주입되어야 한다. (비록 그림 1-4에는 나타나 있지 않지만 이때 신호를 받을 수 이는 코일은 Ho 와 H1의 각각에 대해서 직각인 방향에 놓여야 한다. 즉 Ho 인 외부자장이 z 축에 있다면 그리고 x 축에서 H1 이 주어진다면 리시버 코일 (receiver coil)은 y 축에 놓여진다).

비록 그림 1-4에 나타나 있지 않지만 라디오 파를 발생시키는 코일(또는 oscillatior coil이라고도 부름) 에서 생성되는 작은 자장 H1은 두 가지의 종류가 생성된다. 하나는 그림 1-4에 나타나 있고 다른 하나는 똑같은 진동수를 가지고 있지만 양성자(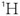)의 세차운동 방향과 반대방향으로 돌고있는 성분이다. 이 성분은 방향(NMR의 용어로는 위상(phase)이라고 함)이 다르기 때문에 고려의 대상이 되지를 못한다.

그림 1-4에서 양성자의 세차운동인 각 속도(angular velocity)와 라디오 파 발생기에서 생성되는 H1의 각 속도(ωo)가 같을 때 세차운동을 하고 있던 양성자는 에너지를 흡수하게 되며 진행하고 있던 세차운동의 축을 벗어나게 된다. 이때 이 성분의 신호를 리시버(receiver)가 받게 된다.

하나는 H1을 서서히 변화(frequency sweep라 부름)시키는 것과 다른 하나는 Ho를 서서히 변화(field sweep)시키는 것이다. 실제로 이 두 방법 중 어느 것을 택하느냐 하는 것은 기기 제작 회사마다 다르며 이 방식의 NMR을 보통 NMR(이 단어에 대한 다른 NMR은 퍽스(pulse)NMR다.) 또는 CW(Continuous Wave) NMR이라고 부른다. 지금까지 양성자 NMR만을 이야기했는데 식 1-6을 사용하여 다른 종류의 핵들도 살펴보기로 하자. 식 1-5와 1-6을 볼쯔만 방정식 1-4에 대입하면 식 1-9가 얻어진다.

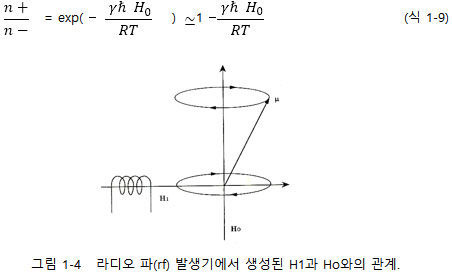
여기서 ℏ는 프랑크 상수 h(Plank's Constant)를 2𝝅로 나눈 것이다. 식 1-9는 낮은 에너지 상태에 존재하는 핵의 수를 결정하는 변수가 우리가 이미 알고 있는 자장의 세기 Ho 이외에 자기회전 비율, 𝜸가 가 직접 참여함을 보여준다. 즉 𝜸가 크면 클수록 식 1-9의 값이 작아지게 되며 이것은 결국 n_상태에 즉, 낮은 에너지 준위에 있는 핵의 수가 증가하는 것이므로 NMR의 감도는 좋아지는 것이다.

표 1-1에 흔히 NMR로 관찰되는 핵들의 여러가지 성질들을 수록하였다.

표 1-1에서 양성자가 자기회전 비율이 가장 큰 것을 볼 수 있다. 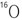와 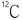은 비록 NMR 현상을 나타내지 못하지만 자연 존재 비의 비교를 위하여 같이 기록하였다. 실제로 탄소는 자연에 미량 존재 하는 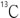만이 NMR의 현상을 나타내므로 감도가 매우 낮지만 NMR에서 가장 많이 사용하는 핵들 중의 하나이다. 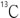의 상대적인 감도를 양성자와 비교할 때 약 1/100을 나타낸다. 자기회전 비가 감도를 나타낸다고 했는데 양성자(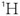)와 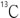의 자기회전 비를 비교해보면 약 1/4이다.

결국 양성자(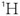)의 공명 주파수에 대하여 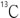의 자기공명을 위한 라디오 파의 진동수는 1/4에 해당( 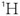이 60 MHz이면 같은 자장 속에서 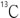은 15 MHz가 됨을 의미함)할 뿐만 아니라 감도도 1/4이라고 생각 할 수 있지만, 궁극적으로 피크를 나타내는 감도는 해당하는 핵이 자연에 존재하는 비(ratio)도 고려하 여야 한다. 즉 표 1-1에 나타난 것과 같이 탄소는 대부분이 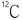즉 NMR 현상을 나타낼 수 없는 핵이고 1.1%의 핵만이 NMR현상을 나타내는 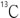으로 존재하므로 결국 양성자 감도의 약 1/100이 되는 것이다.

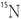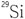표 1-1에서 또 다른 특이한 것은 과 그리고 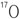의 자기 회전비율이 음의 부호를 가지고 있다는 것이다. 물론 이와 같은 것을 여러 가지 NMR의 현상과 연관하여 설명하는 것은 이 책의 범위를 벗어나는 것이지만 어떤 핵은 이와 같이 음의 자기회전 비를 가진다는 것과 이 핵들은 피크를 얻을 때 다른 핵들과는 좀 다르게 다룬다는 것을 알아두면 차후 NMR을 더 공부하는데 도움이 되리라 생각한다. (제 3장 7절 참조). 표 1-1에 나타난 핵들 중 양성자와 불소를 제외하고는 감도의 문제 때문에 대부분 펄스(pulse) NMR로 만이 측정이 가능하다.

4. 이완(Relaxation)

이제까지 우리는 핵이 에너지를 흡수하여 높은 에너지 상태로 전이를 하는 것을 공부하였다.

그러면 에너지를 흡수한 핵들이 전이를 한 후 어떻게 되는가를 생각해 보기로 하자. 높은 에너지 상태보다 많은 여분의 낮은 에너지 상태의 핵들이 에너지를 흡수하여 높은 에너지 상태로 전이하였다면 더 이상의 에너지의 흡수는 일어나지 않을 것이며, 이 과정이 완료된 것을 포화(saturation)라고 한다. 즉, 이 상태에서는 NMR 피크(net absorption)를 얻을 수 없으며 NMR의 피크를 얻기 위해서는 어떻게 하든 우리는 처음과 같이 낮은 에너지 상태에 핵의 수가 많은 상황을 얻어야 한다. 그러나 다행히도 에너지 를 흡수한 핵들이 에너지를 잃어버리고 처음의 상태로 되돌아오는 현상이 일어나는데 이러한 현상을 이완(relaxation)이라고 한다.

이 과정은 비복사선 과정(radiationless process)으로 일어나며 이때의 속도는 NMR 피크의 넓이 (line width)에 영향을 준다. 또 이때의 속도는 이완 과정의 메카니즘(mechanism)에 따라 스핀-격자 이완, T1(spin-lattice relaxation)과 스핀-스핀 이완 T2(spin-spin relaxation)로 분류된다.

모든 핵들은 특정 범주 내에서 고유의 이완 시간을 가지지만 핵 주위의 환경 그리고 시료의 물리적인 상태에 따라 서로 달라지게 된다. 양성자의 경우 수십 밀리 초(ms)의 시간에서부터 수 초(s)의 경우 가 있을 수 있으며, 탄소의 경우 수십초의 시간까지도 가질 수 있다. 뒤에 더 언급되겠지만 탄소 NMR의 연구 에서 이완시간은 여러 가지 많은 정보를 제공한다. 특히 스핀-격자 이완시간 T1은 이미 언급한 바와 같이 핵 주위 환경 뿐만 아니라 시료의 물리적인 상태에 따라 변할 수 있으므로 때때로 실험에 따라 임의로 증가시켜야 할 때도 있고 감소시키는 경우도 있다. 이러한 실험들을 정확히 이해하고 실험하기 위해서는 그 근본이 되는 이론들을 이해해야 하지만 우리는 여기에서 간단한 이완의 메카니즘만을 정성적으로 다루어 보기로 하자.

핵은 시료를 구성하는 원자들의 집합체인 큰 분자 집단의 일부분이다. 이 커다란 집단은 고체이든 액체이든 또는 기계이든 간에 이들을 격자라고 부른다. 특히 후자의 두 경우 격자를 구성하는 여러 핵은 심한 진동과 회전운동을 하며 각 핵 주위에 복잡한 자기장을 만든다. 이렇게 생긴 여러 자기장 중에 일부는 측정하려 고 하는 핵의 세차운동의 주파수와 위상(phase)에 일치하는 것이 있을 것이다.

결국 이들은 같은 성분의 주파수와 위상을 갖는 핵과 상호작용(resonance)을 할 것이고 높은 에너지 상태에 있는 핵을 낮은 에너지 상태로 바꿀 수 있을 것이다. 그러므로 작은 분자(분자량 (MW) < 200)들의 경우는 진동이나 회전운동이 자유로울 때가 그렇지 못할 때(고체나 점도가 높은 액체에서)보다 T1은 짧아지게 된다. 그러나 고분자(MW = 10000~25000)의 경우는 작은 분자들과는 다르며, 또한 T2는 경우에 따라서는 T1의 분자의 운동에 따른 변화와는 다르게 영향을 받게 된다. 이러한 현상들은 상관 시간(correlation time: 𝝉_𝒄 ) 이라는 것으로 연관되어 설명되어질 수 있으며 이들 또한 제 7 장에서 다시 보기로 한다.

반대로 짝을 이루지 않은 전자(lone pair)를 가진 원소가 있거나 스핀 양자수가 1/2보다 큰 핵이 있을때는 (예를 들면 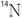, I = 1) 스핀-격자 이완시간 T1은 매우 짧아지게 되는데 이 현상은 비대칭적인 전하 분포를 가짐으로써 생성되는 또 다른 자기장들의 효과 때문에 일어나는 현상이다. 이러한 현상들의 응용은 T1이 매우 긴 시료 속에 상자성(paramagnetic)인 물질을 혼합하여 NMR을 측정하는데 이용된다. 여러가지 실험상에 나타나는 T1 과 T2의 영향은 차후에 더 살펴보기로 하고 여기에서는 가장 쉽게 설명 할 수 있는 피크의 넓이에 관해서 알아보기로 하자.

NMR 피크의 넓이는 이완시간에 반비례하게 되는데 이것은 불확정성 원리(Uncertainty principle)로 설명할 수 있다 (식 1-10).

즉 높은 에너지 상태에 머무르는 평균시간은 T1보다 길 수 없기 때문에 에너지 차이 △E는 h/T1만큼 분포되어야 하고 여기에서 생긴 NMR 피크의 넓이는( v 1/2) 적어도 1/T1의 함수가 되게 된다. 즉 T1이 짧으면 피크의 넓이는 넓어지고 T1이 길면 좁아지게 된다. 그러나 실제의 NMR 피크는 T1에 의해서 예측되는 넓이보다 더 넓어지게 되는데 이것은 T2에 의해서 일어나는 현상이다. T2 또한 불확정성 원리에 따를 수 있으며 식 1-11로 주어진다.

이 때 ν 1/2 은 피크의 중간위치의 넓이를 말한다. T1은 세로 이완(longitudinal relaxation) 시간, T2는 가로 이완(transverse relaxation) 시간이라고도 부르며, 이들의 의미는 거시적 자기화(macroscopic magnetization)로 잘 설명될 수 있으며, 이들의 의미는 의미는 다음 절에서 살펴보기로 하자.

5. 거시적 자기화(Macroscopic Magnetization)

먼저 거시적 자기화가 무엇인가에 대해서 살펴보자. 이제까지 우리는 핵 하나에 대하여 많은 설명을 해왔다. 그림 1-1과 1-3 등은 하나의 핵에 대한 설명의 예로 들 수 있다. 그러나 우리는 하나의 핵만은 결코 실제 시료에서 다룰 수 없다.

아무리 적은 양의 시료라고 하더라도 그것은 어떤 범위의 아보가드로 수(Avogadro's number)만큼의 핵을 포함하게 될 것이다. 이 많은 수의 핵들을 각각 다룬다는 것은 매우 복잡하며 이들을 한데 묶어서 취급할 수 있다면 매우 편리할 것이다. 실제로 각 핵들은 각각의 자기모멘트를 가지고 외부의 자장 Ho에 대해서 세차운동을 할 것이며 이들을 백터로 취급하면 그림 1-5와 같이 표현할 수 있을 것이다.

볼쯔만 방정식(식 1-4)에 따라 높은 에너지 상태와 낮은 에너지 상태에 분포된 벡터들의 합은 결국 낮은 에너지 상태의 벡터 몇 개만이 남아 있게 될 것이며 이들의 합을 벡터 M으로 표시할 수 있을 것이 다. 이때의 벡터 M을 거시적 자기화 벡터라고 부르며 NMR의 여러 현상을 설명하는데 매우 편리하다. 앞 절에서 언급된 세로 이완(T1)과 가로 이완(T2)을 이것으로 설명하여 보자.

그림 1-6에 거시적 자기화 벡터 M과 라디오 파(rf) H1의 상호작용을 보여주고 있다. 처음 거시적 벡터 M은 z축에 존재하게 되며 x축과 y축에는 벡터의 양을 가지지 않는다.

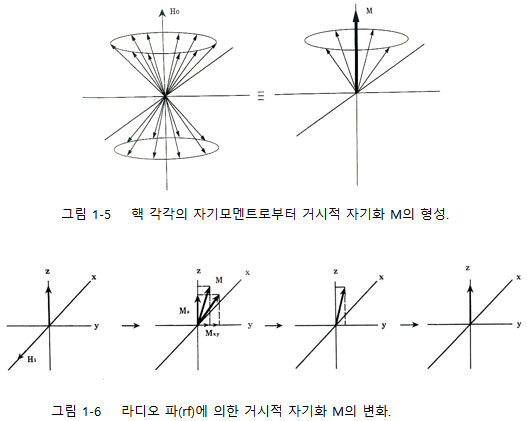
그러나 이 벡터 M에 라디오 파 H1을 주게되면 공명(resonance)의 현상이 일어나면서 벡터M은 z축을 벗어나게 되고 새로운 벡터인 Mxy가 xy의 평면에 만들어지게 된다. 이때 물론 M(Mz)은 줄어들게 된다. 그러나 H1이 존재하지 않게 되면 Mz는 서서히 원래의 크기로 돌아가게 되며(relaxation) Mxy는 서서히 사라지게 된다. 이때 Mz가 원래의 상태로 돌아갈 때 걸리는 시간이 T1이고 Mxy가 없어지는데 걸리는 시간이 T2이다. 이들 각각에 이름 붙여진 세로(longitudinal)이완과 가로(transverse)이완은 위의 설명으로 쉽게 연관 지어질 수 있다.

결국 NMR 실험은 Mxy의 성분을 가지고 있지 않은 거시적 자기화 벡터M을 그 원래의 위치인 z축에서 벗어나게 하여 xy 평면상에 자기의 성분을 생성시킴으로써 y축에 놓여있는 리시버 코일(receiver coil)에 전기적시그날(signal)을 일으키게 하는 것이다. 이때 이 시그날을 일으키는 xy 평면상의 자기 성분은 두 가지 방법으로 만들 수 있다.

하나는 CW(Continuous Wave) 즉, 약한 라디오 파(rf field, H1)를 서서히 변형시켜 라모어 진동수 ωo를 만드는 것이고 다른 하나는 매우 강한 라디오 파(rf pulse라고 부름)를 매우 짧은 시간 동안(µs = microsecond) 주는 방법이다. 이들의 첫 번째 방법을 사용하는 것을 CW-NMR 실험이라 하고 두 번째 방법을 사용하는 것을 펄스(pulse)NMR 실험이라고 한다.

<알림> 본 내용은 이석근 박사님의 저서 "핵자기공명 분광학"의 처음 부분이므로 이후 자세한 내용은 저서를 구매하여 공부 해 보시기 바랍니다.